Solving the 10 Perfect Clears Challenge in Tetris

A journey with Rust and WebAssembly.

25 Dec 2022

Introduction

Modern Tetris poses a unique challenge known as the 10 PC — clearing 40 lines by achieving 10 consecutive perfect clears (PCs), where no filled cells remain on the board after a line clear. Mastering this feat requires hours upon hours of practice, memorization, and effort, making it one of the most difficult tasks in the game (besides quitting Tetris of course).

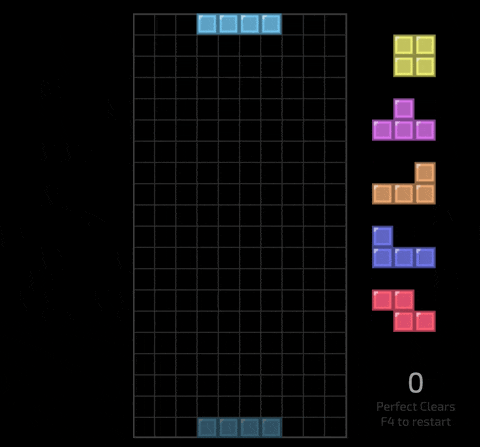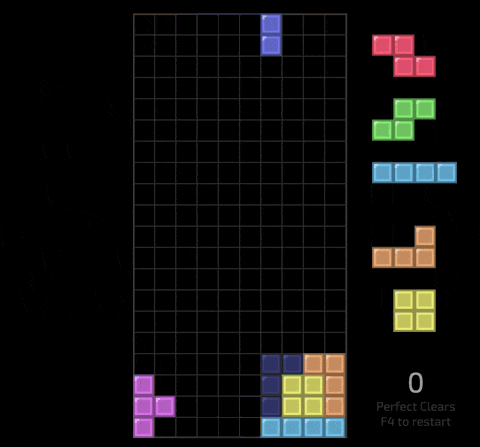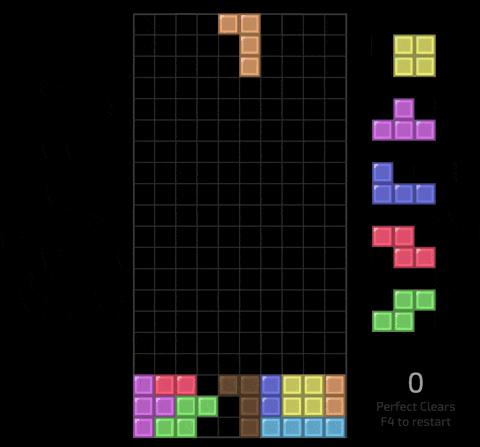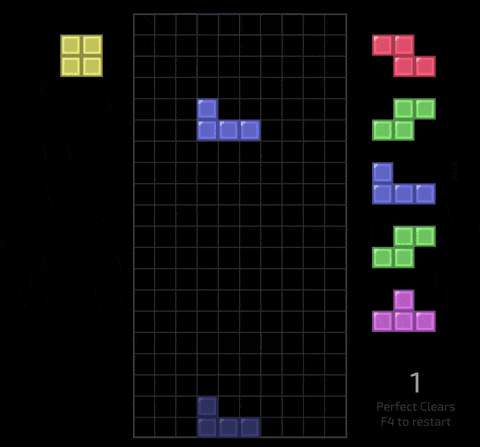
As a computer science student with too much time on their hands, I figured it would be fun to build a tool I could use to tackle this challenge by finding solutions in real time, all within the comfort of a web browser.

Why WebAssembly?

Given the computational intensity of solving 10 PCs, I knew I needed a solution that could run efficiently in a browser. JavaScript, while versatile, wouldn’t suffice due to performance constraints. Enter WebAssembly, a binary instruction format that allows code written in low-level languages like C or Rust to run at near-native speed in the browser. Gone are the days when we needed to download and install desktop applications for native performance. With WebAssembly, we can achieve the performance needed for real-time computations without compromising on ease of access.

Having dabbled in Rust, I saw this project as the perfect opportunity to put my skills to the test. Rust’s performance, safety features, and excellent support for WebAssembly through the wasm-bindgen library made it the ideal choice for building my Tetris solver.

The Challenge of 10 PCs

When starting a Tetris game, you see an active piece and a queue with the next 5 pieces. Each piece comprises 4 cells, and with the board being 10 cells wide, achieving a perfect clear means placing 10 pieces to fill 40 cells within 4 lines.

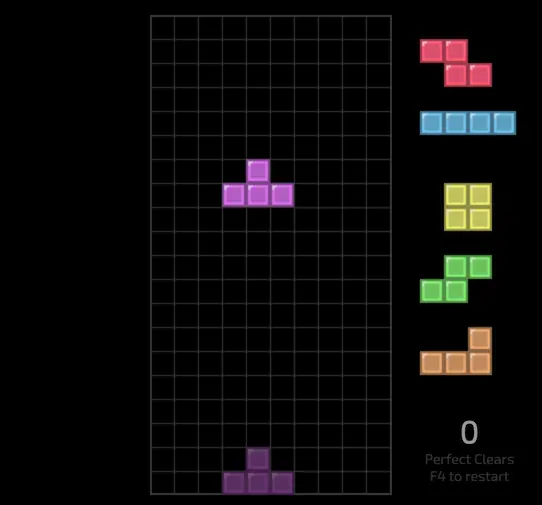
Given the SRS (Super Rotation System) rules, which use a 7-bag system (where each bag contains all 7 Tetris pieces), the probability of encountering specific sequences is not uniform. My strategy was to leverage this system to calculate the likelihood of seeing particular sequences and recommend the best moves to achieve a perfect clear.

Since you only see 6 pieces at the start of the game, the last 4 pieces to make a perfect clear must be determined stochastically. Therefore, the process looked simple enough:

1. use a backtracking search algorithm to explore all possible moves given the visible and guessed pieces,
2. find all move sequences that end in a perfect clear and their associated probabilities,
3. group sequences based on their first move and sum their probabilities,
4. recommend the move with the highest summed probability to the player,
5. when the player places a piece and reveals the next piece in the queue, filter out sequences that are no longer possible, and update the probabilities.

What could go wrong?

Building the Solver

Board representation

A Tetris board comprises 22 rows of 10 cells (20 visible rows and 2 hidden rows above the visible board) where each cell is either filled or empty. Each cell can be either filled or empty, allowing the board to be represented as a bitfield with 220 bits. Since the largest integer supported in WebAssembly is 64 bits, 4 u64 values are required to represent a full board.

However, for solving perfect clears, we only need to track the bottom 4 rows plus 2 hidden rows above, reducing the board to 60 cells, which can fit into a single u64.

struct Board(u64);

This compact representation allows for quick bitwise operations, essential for high-performance computations.

Positioning and rotating pieces

There are a multitude of different rulesets for Tetris which affect how pieces behave and interact with the game, but the most popular variant in modern Tetris is the Super Rotation System (SRS). The rulesets define the behavior of Tetris pieces, including their spawn orientation, rotation, and wall kicks (what happens when a piece collides with a filled cell when rotating). A key challenge in implementing these rules was handling half-integer coordinates, which occur when a piece’s center of rotation lies between cells.

To simplify this, I treated the position as the bottom-left-most cell of a square bounding box and standardized rotations as rotations within a 3x3 or 4x4 bounding box. This approach preserved the SRS behaviors while eliminating the need to track half-integer coordinates, making the code more straightforward and efficient.

Solver state machine

The solver is designed as a state machine with three stages:

1. Inactive Piece Stage: Determines the solver’s next piece by either consuming the next piece in the queue or guessing it.
2. Active Piece Stage: Moves the active piece to all possible positions and orientations where it can be placed on the board.
3. Decision Stage: Recommends the best move to the player based on the calculated probabilities of achieving a perfect clear.

For example, here’s how the solver branches a current state into multiple possible next states when considering the next piece:

fn branch_state_for_piece(config: &Config, state: &State) -> Vec<State> {
    // An active piece already exists, return the current state.
    if state.game.piece.is_some() {
        return vec![state.clone()];
    }
    // Try to consume the next piece in queue.
    if let Ok(state_after_consume_queue) = state.reduce(config, &Action::ConsumeQueue) {
        return vec![state_after_consume_queue];
    }
    // Otherwise, guess the next piece.
    PIECE_KINDS
        .iter()
        .filter_map(|&kind| {
            if state.piece_probability(kind) < 0.01 {
                return None;
            }
            match state.reduce(config, &Action::WithNextPiece { kind }) {
                Ok(state) => Some(state),
                Err(_) => None,
            }
        })
        .collect()
}

Performance Challenges

Naive approach

Initially, I used a brute-force method, recursively exploring all possible states by branching out from each move. However, this approach was computationally expensive. To put it into perspective, assuming there are no pieces in the queue, we have to:

• guess approximately 7 possible next pieces for 7 states,
• account for the hold piece which doubles our possible next states to 14 states, and
• check an average of 20 possible placable positions and orientations, increasing the number of possible next states to approximately 280.

For a single perfect clear with 4 guessed pieces, that amounts to a minimum of 6 billion possible states. This made real-time solving unfeasible.

Optimizations

Memoization in a graph

Many sets of actions can result in the same solver state. To avoid recalculating results for states that had already been explored, I implemented memoization using a graph structure (implemented by the wonderful petgraph crate) and a HashMap<SolverState, NodeIndex>. This optimization significantly improved performance but was still not enough for real-time execution.

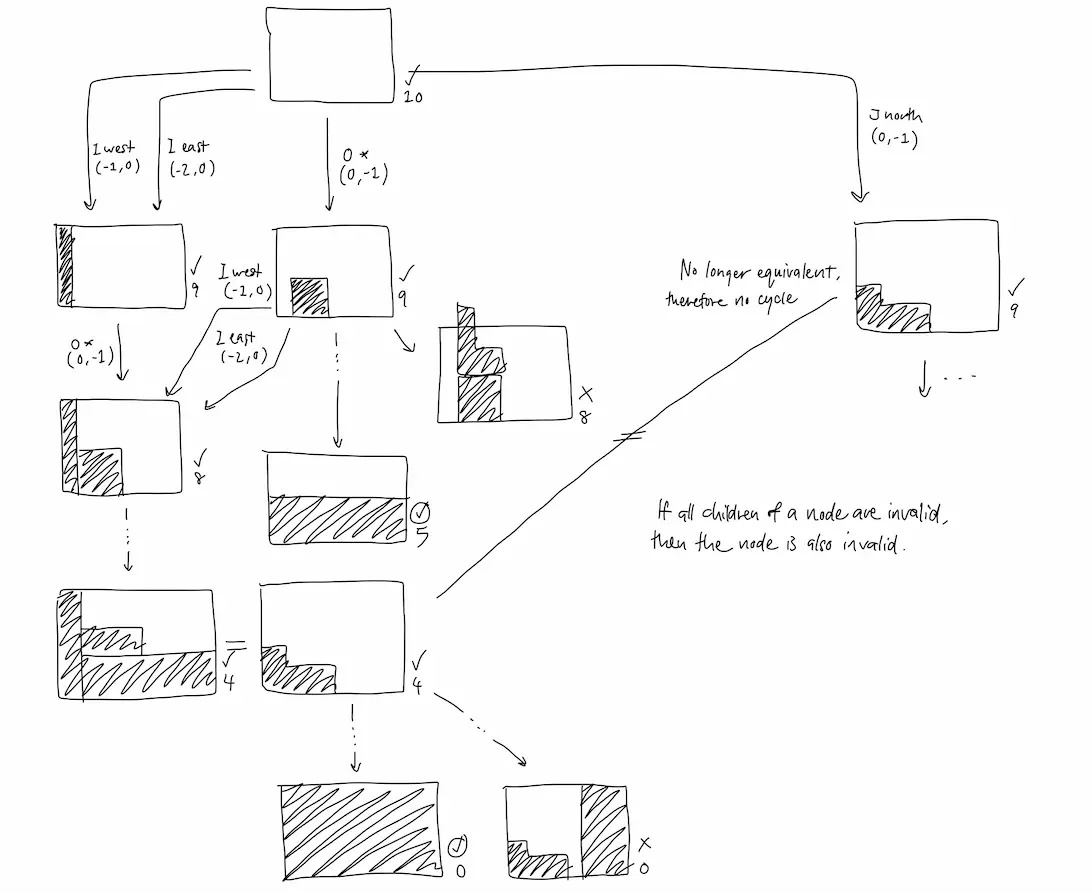
Pruning Invalid States

Another key optimization was to prune branches where pieces were placed above the bottom 4 rows. These states would never result in a perfect clear, so eliminating them early saved considerable processing time. On my 2017 MacBook Pro, this brought the average time to find the first perfect clear down to 5 minutes — better, but still far from real-time.

Future improvements

At this stage, I decided to take a break from the project. While the solver’s current performance is not where I want it to be, there’s a clear path forward: integrating memorized patterns and optimizing memory usage.

Leveraging Memorized Patterns

As of 2022, the record for most consecutive perfect clears belongs to Holifyre with 312 perfect clears under an hour.

Experienced Tetris players often rely on setups and memorized solutions to achieve perfect clears. As Clcck puts it, “70% […] comes down to memorised setups/solutions, [and] the other 30% [is] based on feel and understanding of how 7-bag works”.

10 PC guides exist, but I did not spend the time to learn them or understand how perfect clears are solved by regular players. By incorporating these patterns into the solver, I could have drastically reduced the computational load, potentially achieving the real-time performance I initially aimed for.

Reducing heap allocations

Another area of improvement lies in memory management. I noticed that I used heap allocations unnecessarily throughout the code. While the solver strategy itself was flawed, I could have also optimized the use of data structures to reduce the need for frequent vector allocations. For example, preallocating vectors with a known maximum size or using stack-based data structures could significantly reduce memory overhead and improve performance. This change would also make the solver more efficient in terms of both speed and memory usage.

Conclusion

This project has been a deep dive into algorithmic efficiency and the trade-offs between brute-force solutions and more optimized approaches. While I set out with the belief that raw computing power could overcome the challenge, I learned the importance of leveraging existing knowledge and strategies.

This is my first project which focuses on algorithmic efficiency and performance, and my mistakes clearly stand out. However, if you’re interested in exploring the code as it stands during the time of this post, feel free to check out the repository on tag v0.1. Moving forward, I plan to continue refining the solver, hopefully transforming it into a valuable tool for Tetris players looking to master the 10 PC challenge.